生成式艺术和算法创作08-马尔可夫模型

马尔可夫模型 Markov Model

开始的开始，有必要来认识一下主人公，俄国数学家安德雷·安德耶维齐·马尔可夫。

1874 年，18 岁的马尔可夫考入圣彼得堡大学，师从切比雪夫（著名的切比雪夫定理提出者）。他是物理-数学博士，圣彼得堡大学教授，圣彼得堡科学院院士。在概率论、数论、函数逼近论和微分方程等方面卓有成就。

总的来说，马尔可夫模型是一种统计模型，可以用于计算条件概率分布，为一系列的离散事件建模。这就应用很广泛了，哪些是「离散事件」呢？句子中的词汇，音乐中的音符，通过交通灯的车辆数，女票每个月购物的次数……

以「马尔可夫」开头的术语有很多，先来熟悉一下最重要的几个：

马尔可夫性质：当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态。
马尔可夫过程：是一个具备了马可夫性质的随机过程，不具备记忆特质（memorylessness）。换言之，马可夫过程的条件概率仅仅与系统的当前状态相关，而与过去历史或未来状态，都是独立、不相关的。
马尔可夫链：具备离散状态的马可夫过程，通常使用离散的时间集合定义。
马尔可夫模型：用马尔科夫过程生成序列的算法模型

它们之间的关系大概可以这样划分：

	系统状态是完全可观察的	系统状态是部分可观察的
系统是自治的	马尔可夫链	隐马尔可夫模型
系统受到控制	马尔可夫决策过程	部分可观察的马尔可夫决策过程

在马尔可夫模型中

$X_t$ 是时间 t 时表示音符的随机变量
$P(X_t)$ 是随机事件 $X_t$ 的概率分布

马尔可夫模型可以基于「上文」做出判断和预测，未来状态只取决于当前状态或者限定范围的过去状态。

实现马尔可夫模型的学习算法有几个步骤：

构建一个 transition count table (state transition matrix)，计算每一种可能的上下文的频率分布
用每一种组合的 count 除以所有的组合总数，即下表中每一行加起来为 1
随机选择一个起始值，根据概率表格选择下一个序列值

马尔可夫模型生成算法其实也是一种 random walk ，根据转换概率分布，基于目前已经生成的序列，随机选择下一个序列值。

以一段乐曲为例，它由音符 B2,C4#,D4,E4,F4#,G4,G4#,A4,B4,C5#,D5,E5 组成。计算每一个音符后面紧跟着的音符的出现概率。例如，最后一个音符 E5，出现在它后面的音符只有 A4 和 C5#，出现概率分别是 6/16 和 10/16。当生成新的序列时，如果当前音符是 E5，那么根据表格，下一个音符只可能是 A4 或 C5#。

song corpus

再来看一个三节点的马尔可夫链：

这首马尔可夫旋律以 state_0 开始，播放一个八分音符 Eb。然后选择一个新的状态。选择 state_0，state_1 或 state_2 的概率相等，都是 1/3。假设选择了 state_2，则播放下加二间的十六分音符 G。从 state_2 开始，state_0 被选择的概率是 1/10，state_1 是 2/10，state_2 是 7/10。

因为马尔可夫模型状态是离散的，可以用有限状态的自动机 (automata) 来表示。

markov models automata representation

变量马尔可夫模型

在随机过程中，变量马尔可夫（Variable order Markov Models/VOM/VMM/VOMM）模型是一类重要的模型，它扩展了马尔可夫模型。

马尔可夫模型中，具有马尔可夫性质的序列中的每个随机变量，取决于固定数量的随机变量；在 VOM 模型中，该数量的调节随机变量可以基于观察到的特定实现而变化。

这个实现序列通常被称为上下文 ; 因此 VOM 模型也称为上下文树。调节随机变量数量的灵活性对于许多应用来说是非常有利的，例如统计分析、分类和预测。

变量马尔可夫模型一般由三部分组成：

Counting：建立转换表，这是预测的来源
Smoothing：处理未见过的事件/序列
Variable length modeling:
- A transition matrix
- Probabilistic suffix tree
- Factor Oracle, and Context Tree Weighting method (CTW)
- Lempel-Ziv 78 and its improvement LZ-MS
- Prediction by partial match

它的缺点之一是难以产生语料之外的内容。

隐马尔科夫模型 Hidden Markov Model

隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数，然后利用这些参数来作进一步的分析，例如模式识别。

在一般的马尔可夫模型中，状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。

而在隐马尔可夫模型中，状态并不是直接可见的，但受状态影响的某些变量是可见的。每一个状态在可能输出的符号上，都有一定的概率分布。因此输出符号的序列能够透露出状态序列的一些信息。

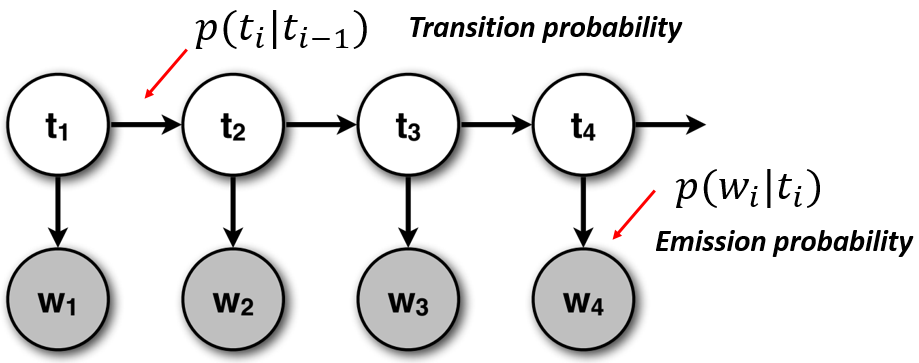
也就是说，HMM 系统的实际状态是隐藏的，只能观察到 emission probilities。

HMM 常用来学习两个耦合的内容语料。例如，在语音识别中，可见的信息是音频信号，隐藏的信息是语音词汇。又例如，旋律是可见信息，伴奏/ 和声是隐藏的信息。

最常见的三种 Hidden Markov Model 算法：

the forward algorithm: 计算特定序列的概率，假设已知 transitions and observation 概率和初始状态
the Baum-Welch algorithm：找出被观测序列中最常见的参数
the Viterbi algorithm：维特比算法，基于观测序列计算隐藏状态最可能的序列（viterbi path）

隐马尔科夫模型的优势：

是学习和生成离散序列最有效和使用广泛的算法
可以对横轴和纵轴的相关性都建模，HMM 是随机耦合过程
比马尔可夫模型更好保留原始的数据结构

劣势：

需要有很好的领域知识来调整模型结构和参数
需要相对大的训练数据集

马尔可夫模型在音乐中的应用

Lejaren Hiller 在 1957 年完成了算法生成的弦乐四重奏「依利亚克组曲」（Illiac Suite），这也是历史上第一支完全由计算机生成的音乐作品。首先使用马尔可夫链模型来产生有限控制的随机音符，之后利用和声与复调的规则测试这些音符，最后选择符合规则的材料，修改、组合成传统音乐记谱的弦乐四重奏。

ILLIAC Suite