生成式艺术和算法创作03-混沌和分形

生成式艺术和算法创作01-概述

生成式艺术和算法创作02-随机和噪声

动态系统

动态系统（dynamical system）是数学上的一个概念，是一种固定的规则，它描述一个给定空间中所有点随着时间变化的情况，例如运动的钟摆、弹跳的球、管道中水的流动等。

动态系统的行为可以分为四类：

Fixed point behavior (equilibrium)：固定（平衡）行为
Limit cycle or periodic behavior：循环或周期行为
Quasi-periodic behavior：准周期行为
Chaotic behavior：混沌行为

虽然动态系统是可以确定的，但是一旦输入发生微小改变，结果都会变得难以预测。混沌系统短期、局部可预测，长期、全局不可预测的特点，让它成为算法创作中常用的手段。

via Generalization of the simplest autonomous chaotic system

单峰映象（logistic map）是一个二次的多项式映射，是由简单非线性方程式产生混沌现象的经典范例。

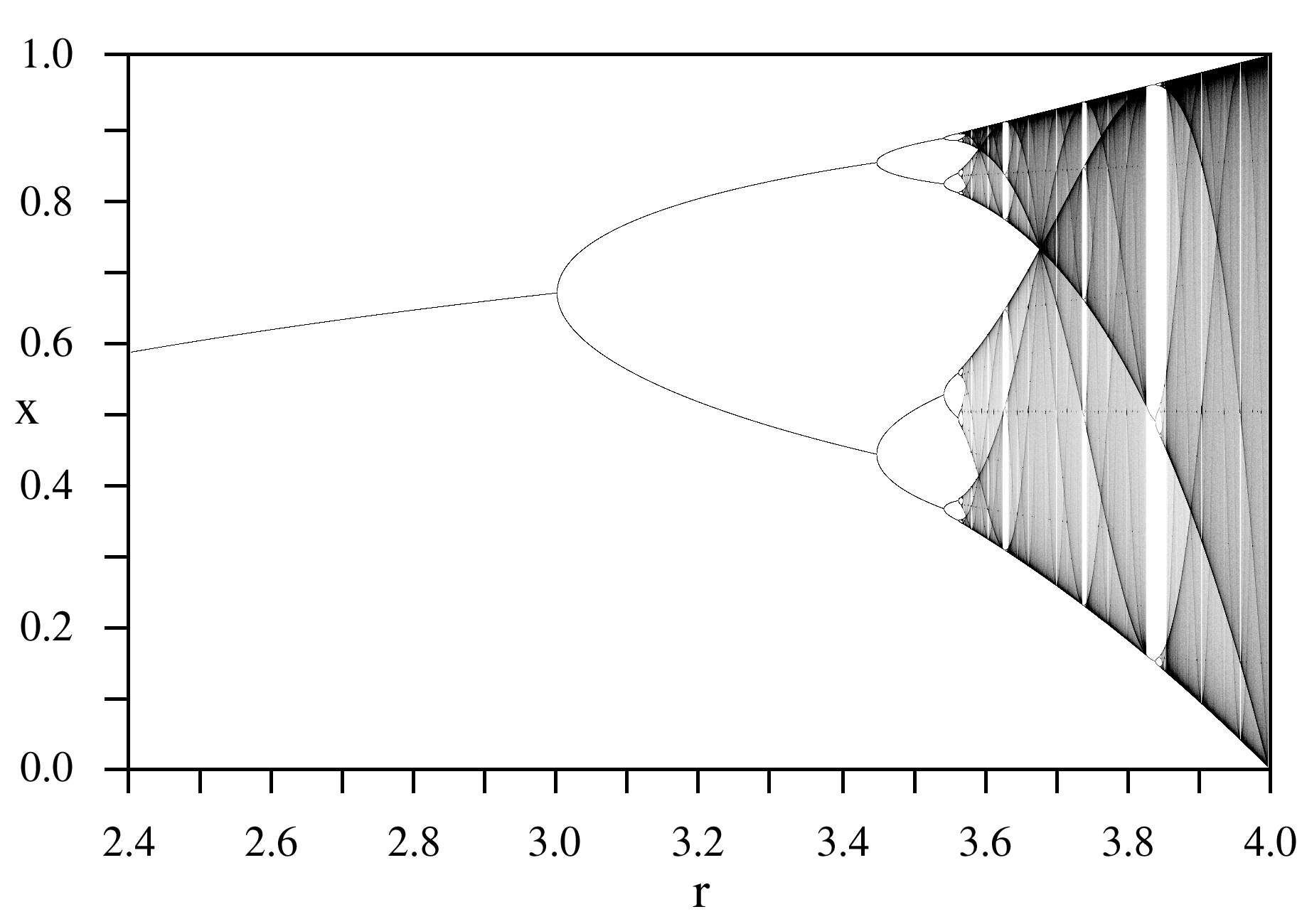
这种映射因生物学家 Robert May 在 1976 年发表的一篇论文而著名。公式为 $$x_{n+1}=rx_n(1-x_n)$$。对于任一个 r 值，最多只有一个稳定的极限环，若稳定极限环存在，几乎所有的点最后都会趋近极限。这些情况可用分枝图表示，分枝图中的横轴是 r 的数值，纵轴中显示大部份初值下稳态可能的 x 值，若数值在 2 个值中震荡，分枝图上对应的数值就会有 2 个点。若某 r 值已无法明确有几个对应的点，系统可能已经处于混沌状态。

分枝图有自相似的特性。若将分枝图中 r=3.82 的部份展开，只取三个分支中的一个，图形会好像是原分枝图缩放及扭曲后的结果。所有非混沌的参数 r 都有此一特性。可以看出混沌和分形的关系。

吸引子（attractor）是微积分和系统科学论中的一个概念。一个系统有朝某个稳态发展的趋势，这个稳态就叫做吸引子。

吸引子分为平庸吸引子和奇异吸引子。例如一个钟摆系统有一个平庸吸引子，这个吸引子使钟摆系统向停止晃动的稳态发展。平庸吸引子有不动点（平衡）、极限环（周期运动）和整数维环面（概周期运动）三种模式。不属于平庸的吸引子的都称为奇异吸引子，它表现了混沌系统中非周期性，无序的系统状态，例如天气系统。目前吸引子在学术上还没有完善的定义，奇异吸引子对于混沌系统的研究意义重大。

混沌理论的思想也从上世纪后半叶开始，逐渐渗入到音乐和作曲领域。

1960 年 George Brecht 在滴水事件（drip event）中，使不同来源的水，滴进所有空的容器。这个作品可以被视为音乐、剧场、或者是动态雕塑。

Brecht 的极简主义艺术活动是神秘费解、令人困惑的，这些作品及其配乐为观众设计成仅在想象的范围内可被解读与激活。滴水音乐（drip music）由此形成，指可由单个或多个表演者演出单一滴水水源与一个空的容器，通过设置使水滴入容器中。Drip music 很快就成为激浪派（fluxus）的标志，flux 一词本身不仅指持续的运动与改变，也指流体与流动，或更精确的是一个流体的流动速度。

80 年代，混沌理论开始被应用在作曲中。它适用于音高、持续时间、动态范围和编排。它们很容易产生重复，以及周期性/准周期性模型变化，或者在混沌模式下产生更多不可预测的行为，而重复、变化、convergence 和 divergence 是音乐作曲里的关键要素。

分形

分形是一个可以分成数个部分的几何形状，且每一部分都（至少近似地）是整体缩小后的形狀，即具有自相似的性质。分形也被称为扩展对称或展开对称。如果在每次放大后，形状的重复是完全相同的，被称为自相似。作为一个数学函数，分形通常是处处不可微的。无穷分形曲线可以理解为一条一维的曲线在空间中绕行。

Fractals are mathematical dynamic systems represented by iterative equations that develop curves and geometrical shapes that have property of self-similarity.

Sierpinski 三角是典型的自相似分形图形。1915 年由波兰数学家 Wacław Franciszek Sierpiński 提出。