
阿扣:上一次我们了解了损失函数。为了找到使损失函数(比如用 SSE 计算)最小的 w (权重) 和 b (偏置项),我们需要先了解一个重要的方法:梯度下降。
阿特:听起来像坐滑滑梯~
阿扣:是有那么点意思。
阿扣:想象一下,我们对网络中的一些权重做了很小的改变,这些变化会让输出也有相应很小的变化:
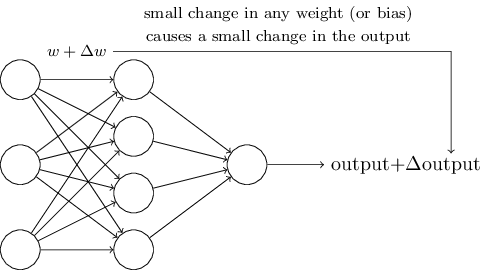
via Neural networks and deep learning - chapter 1
然后拿这些微小的变化,跟目标值对比,看看误差是变大还是变小了,然后不断调整权重值,最终找到最合适的 w 和 b。
阿特:那要怎么找到这些值呢?
阿扣:下面有请「梯度下降」 Gradient Descent。
阿特:终于能坐滑滑梯了……
阿扣:坐这个滑滑梯可能有点晕 😄 。我先给你打个比方。想象一下,你在一个山峰的山顶,想用最快的速度到达山脚。
阿特:坐缆车可以吗?
阿扣:缆车,不存在的……只能靠走的。要往哪边下山呢?我们会选一个看起来「下降」最快的路径:

朝这个方向走一段后,我们再看下一步往哪个方向走,「下降」最快。

一直重复这个过程,就能最快的速度下到山脚。
阿特:是这么个道理。
阿扣:这个方法,就是「梯度下降」,在机器学习中很常见。所谓「梯度」,其实是指「变化率」或者「坡度 slope」,就是多变量函数的导数。
阿特:导数?!你说的是微积分里面那个导数吗? …… 瑟瑟发抖.gif
阿扣:别紧张,先听我讲,回忆回忆。
阿特:好吧。
阿扣:你还记得怎么表示函数 f(x) 的导数吧?很简单,就是 f’(x) 。
阿特:嗯嗯,记得。
阿扣:所谓「梯度」,其实就是函数在某一点上的变化率,根据微分的知识,变化率可以通过这一点的切线求得,而切线其实就是函数的导数:f’(x)。

来,跟我念一遍:求梯度 = 求变化率 = 求导数
阿特:求梯度 = 求变化率 = 求导数 (假装自己听懂了)
阿扣:了解了「梯度」,然后我们来看看「下降」又是怎么回事。
切线代表函数在某个点的变化率。在上面这个图中,x = 2 位置上的切线,斜率是 > 1 的。说明如果继续往 x = 2 的右边滑去,在曲线上的值就会变大。比如当 x = 3 时,y = 9。
但是我们想要到曲线最低的地方去,因为那里可以让误差(也就是 cost )最小。所以,应该沿着梯度「相反」的方向滑动,也就朝着是 x = 2 的左边滑去。这就是「下降」的含义。
阿特:沿着「上山」最快的反方向走,就能最快「下山」。啊原来这么直白……
阿扣:对呀,原理并不复杂的。
这个视频讲解了线性回归和梯度下降的关系,来看看吧!
Linear Regression Answer - YouTube
阿特:这个视频不错,讲得挺清楚的~
阿扣:我们来复习一下。用一个函数 f(h) 表示 x 和 y 的关系。x 和 y 其实是已知的,它们来自真实的数据集。我们的目标是求出 w 和 b,使得计算出来的 $\hat y$ 最接近实际的 y 值。为了得到某种类型的 y 值(比如只有 0 和 1 两种输出),我们会使用类似 Sigmoid 这样的激活函数,对 f(h) 做一下转换。

阿特:哦,我说怎么有点难理解呢。因为以前碰到 x 和 y,它们都是未知数,现在它们变成了已知数,真正的目标其实是求 w 和 b!
阿扣:没错!这是深度学习算法中一个需要调整的认知。
怎么得到 w 和 b 呢?用损失函数。如果损失函数的值大,说明模型预测得不准。我们要找到让损失函数的值最小的 w 和 b。更具体说,我们要找到 w 的变化幅度 $\Delta w$,每次调整一小步,看看误差 E 是不是变小了。

为了求出 $\Delta w$,我们引入「误差项」$\delta$ ,它表示 误差 * 激活函数的导数。然后用「误差项」$\delta$ 乘上学习率 $\eta$ (用来调整梯度的大小),再乘上 x,就是每次应该调整的权重值 $\Delta w_{ij}$

阿扣:比如说,如果激活函数是 Sigmoid 函数。
$$ f(h)=\frac {1}{1 + e^{−h}} $$
$$ f’(h)=f(h)(1−f(h))$$
$$ \Delta w_{ij}=\eta(y_j-\hat y_j)f(h)(1−f(h))x_i $$
…… 咦?人呢?
喂!别跑,还有好几个知识点没讲呢!……
补充:求多个变量的偏导数
如果只有一个未知数,求梯度只需要计算导数。如果有多个变量,求梯度就需要计算偏导数。偏导数其实并不复杂,只需要掌握链式求导法则,就能进行大部分的计算。
$$ \frac{\partial}{\partial w} p(q(w)) = \frac{\partial p}{\partial q}\frac{\partial q}{\partial w} $$
比如,损失函数 C
$$ C = \sum(wx + b - y)^2 = \sum((wx + b)^2 + y^2 - 2y(wx + b)) = \sum(x^2w^2 + b^2 + 2xwb + y^2 - 2xyw - 2yb) $$
对 w 求偏导
$$ \frac{\partial C}{\partial w} = \frac{1}{N} \sum(wx + b - y)x $$
对 b 求偏导
$$ \frac{\partial C}{\partial b} = \frac{1}{N} \sum(wx + b - y) $$
Ref
- Deep Learning Nanodegree | Udacity
- Neural Networks and Deep Learning | Coursera
- Gradient Descent with Squared Errors
- Gradient (video) | Khan Academy
- An overview of gradient descent optimization algorithms

