
回顾:
阿扣:阿特,今天我们来了解一下深度学习中的激活函数(Activation functions)。
阿特:又是函数……为什么要了解这个哦……
阿扣:在机器学习中,我们经常需要对输出结果打上「是」或「否」标签。比如对一张输入的图片,模型要判断图片里面有没有包含汪星人。

上一回我们提到的逻辑回归,可以用来减少预测值和真实值之间的误差。
阿特:那要怎么做呢?
阿扣:我们来用符号描述一下问题:
- x:训练数据中的 input
- y:训练数据中已经做好标记的 output
- w:逻辑回归的 weights
- b:逻辑回归的 bias
- 模型的输出:$\hat y = \sigma (wx + b)$
阿特:老朋友 wx + b
阿扣:好眼力。它就是一个线性模型。别忘了,我们想让输出只包含两个值:是,否。一般我们会用 1 表示「是」,用 0 表示「否」。
阿特:就是我给模型图片 A,它说「0」;给图片 B,它说「1」;……这样?
阿扣:没错~ 所以我们把结果的输出全部转换成或 0 或 1 的值。激活函数就是用来帮助我们实现这种转化的。
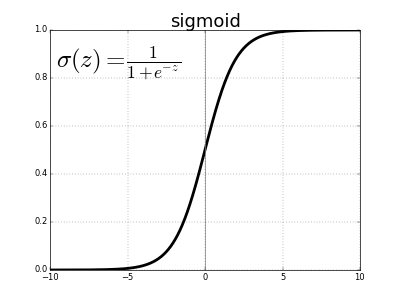
上面我们用到的激活函数叫做 Sigmoid 函数。它帮我们做到了:
- 如果输入值 z 是一个大的正数,函数的输出值为 1;
- 如果输入值 z 是一个大的负数,函数的输出值为 0;
- 如果输入值 z = 0,那么输出值是 0.5
阿特:也就是说,不论我给什么样的整数,最后都会返回 0 或 1 的结果?
阿扣:没错!这样我们得到分类的结果,或 0 或 1。在深度学习中,这种把输出转化为我们想要的形式的函数,我们叫它「激活函数」:
激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。加入激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。
上图就是其中的一种激活函数:sigmoid 函数。
阿特:这么说,激活函数不止一种?
阿扣:对呀。下面我列了一些常用的激活函数,作为今天的补充资料吧。现在可能还看不到,先混个脸熟就好。
阿特:好的先刷脸。
Sigmoid
$$ sigmoid(z)= \frac{1}{(1+e^{−z})} $$
Sigmoid 函数取值范围为(0,1),将一个实数映射到(0,1)的区间,可以用来做二分类。

Sigmoid 在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid 的导数最大值为0.25。这意味着用来进行反向传播时,返回网络的 error 将会在每一层收缩至少75%(梯度消失问题)。对于接近输入层的层,如果有很多层, weights 更新会很小。
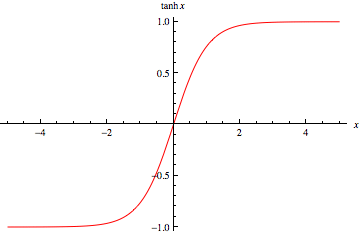
Tanh
$$tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} $$
也称为双切正切函数,取值范围为[-1,1]。tanh 在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
ReLU
$$ReLU(z) = max(z,0)$$
ReLU (rectified linear units) 是现在较常用的激活函数。如果输入 < 0,ReLU 输出 0;如果输入 >0,输出等于输入值。

ReLU 计算量小(不涉及除法),一部分神经元的输出为 0 造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
ReLU 的缺点是,梯度较大时,ReLU 单元可能大都是 0,产生大量无效的计算(特征屏蔽太多,导致模型无法学习到有效特征)。
Softmax
$$ softmax(z) = \frac{e^z{j}}{\sum^K{k=1}e^z{_k}}$$
Softmax 函数将 K 维的实数向量压缩(映射)成另一个 K 维的实数向量,其中向量中的每个元素取值都介于(0,1)之间。常用于多分类问题。Softmax 把分数转换为概率分布,让正确的分类的概率接近 1,其他结果接近 0。相比 Sigmoid,它做了归一化处理。


